@45°夹角的考研力
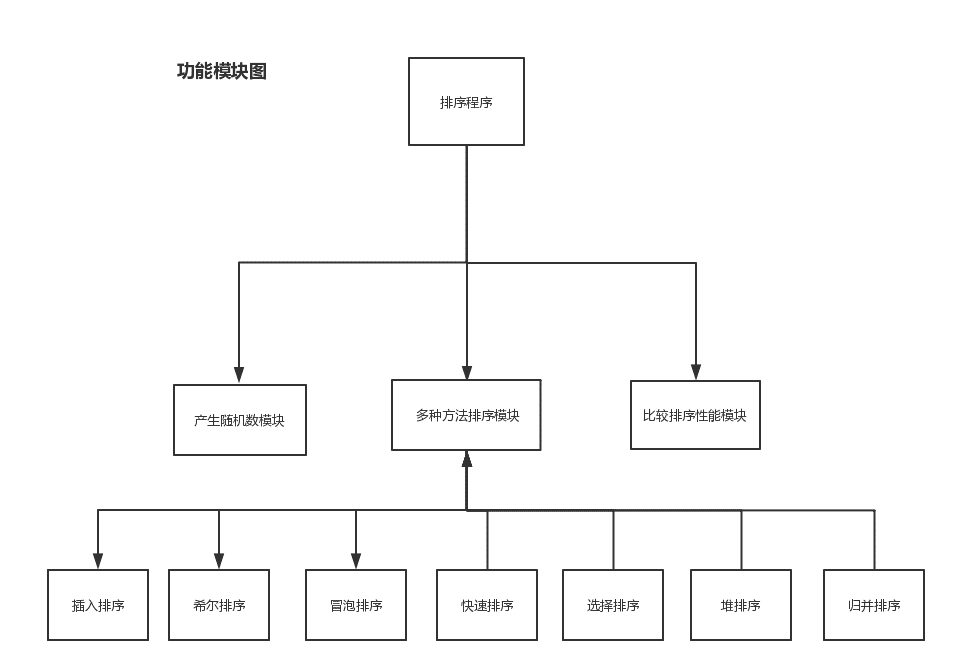
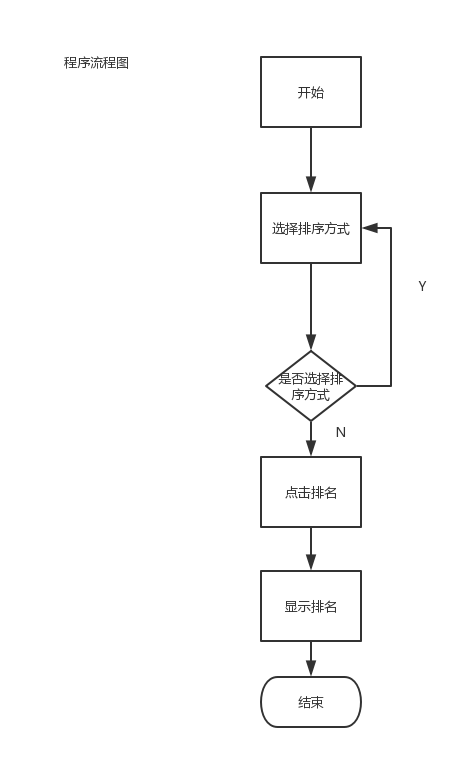
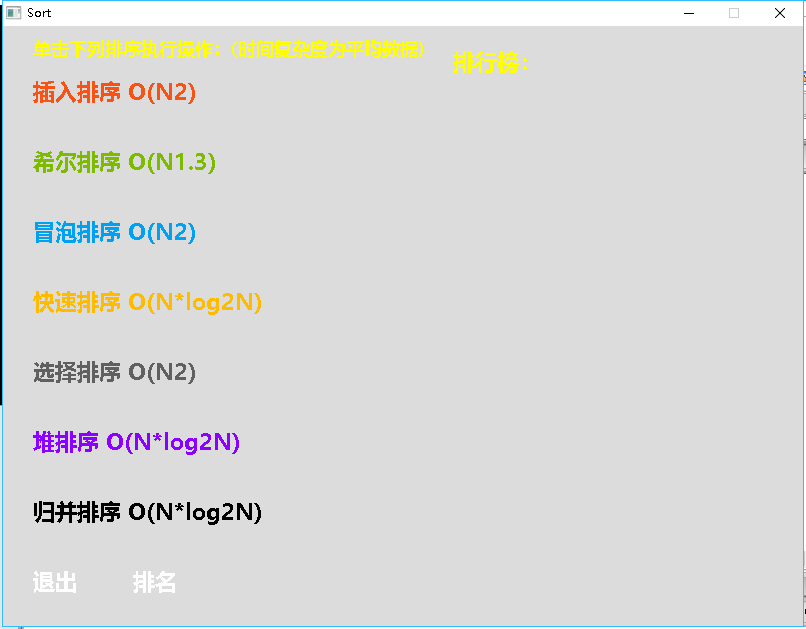
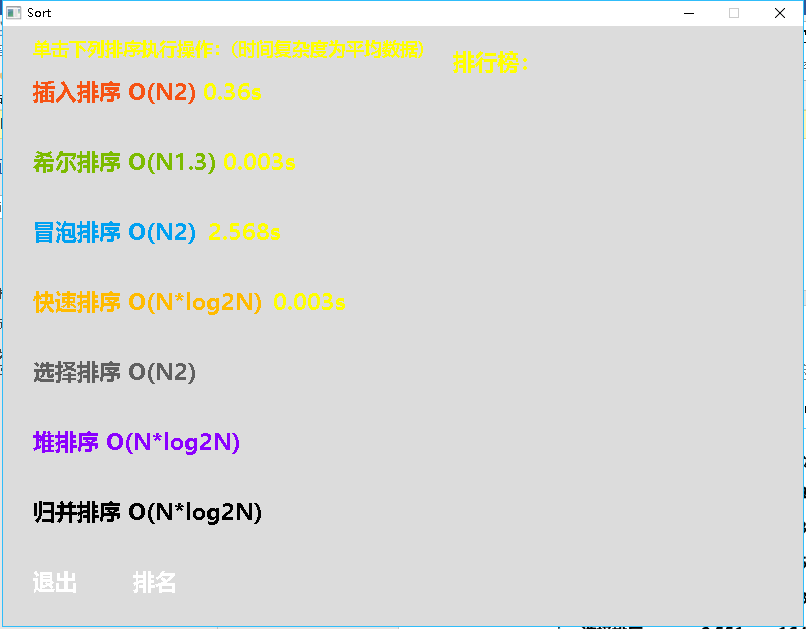
1.只出现一次的数字
class Solution {
public:
int singleNumber(vector<int>& nums) {
int result = nums[0];
for(int i = 1; i < nums.size() ;i++){
result = result ^ nums[i];
}
return result;
}
};2.多数元素
class Solution {
public:
int majorityElement(vector<int>& nums) {
//出现次数超过一半的数字一定是出现最多的数字
map<int , int>mp;
int max = 0;//出现次数
int result = 0;//出现次数最多的数字
for(int i = 0; i < nums.size() ; i++){
if(mp.find(nums[i]) != mp.end()){//map中找得到该数字
mp[nums[i]] = ++mp[nums[i]];
if(mp[nums[i]] > max){
max = mp[nums[i]];
result = nums[i];
}
}
else{//map中找不到该数字
mp[nums[i]] = 1;
if(1 > max){
max = 1;
result = nums[i];
}
}
}
return result;
}
};class Solution {
public:
bool findTarget(vector<vector<int>>& matrix , int i , int j , int target){
if(matrix[i][j] == INT_MIN){//递归可能会超时,需要将递归经过的地方设置为INT_MIN,之后递归再次遇到该值直接跳过;
return false;
}
else if(matrix[i][j] == target){
return true;
}
else if(matrix[i][j] > target){
return false;
}
else{
matrix[i][j] = INT_MIN;
}
if(i == matrix.size()-1 && j == matrix[i].size()-1){//最后一行最后一列
return false;
}
else if(i == matrix.size()-1){//最后一行
return findTarget(matrix , i , j+1 , target);
}
else if(j == matrix[i].size()-1){//最后一列
return findTarget(matrix , i+1 , j , target);
}
if(matrix[i][j] < target && matrix[i+1][j] > target && matrix[i][j+1] > target){
return false;
}
return findTarget(matrix , i+1 , j , target) || findTarget(matrix , i , j+1 , target);
}
bool searchMatrix(vector<vector<int>>& matrix, int target) {
return findTarget(matrix , 0 , 0 , target);
}
};4.合并两个有序数组
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
vector<int> nums3;
int p1 = 0;
int p2 = 0;
while(p1 < m && p2 < n){
if(nums1[p1] <= nums2[p2]){
nums3.push_back(nums1[p1]);
p1++;
}
else{
nums3.push_back(nums2[p2]);
p2++;
}
}
if(p1 == m){
for(int i = p2 ; i < n ; i++){
nums3.push_back(nums2[i]);
}
}
else if(p2 == n){
for(int i = p1 ; i < m ; i++){
nums3.push_back(nums1[i]);
}
}
nums1.resize(0);
for(int i = 0; i < m+n ;i++){
nums1.push_back(nums3[i]);
}
}
};5.验证回文串
class Solution {
public:
bool isPalindrome(string s) {
//大写转换为小写
for(int i = 0; i < s.length() ;i++){
if(s[i] >= 'A' && s[i] <= 'Z'){
s[i] = s[i] + 32;
}
}
int i = 0;
int j = s.length() - 1;
while(i < j){
//筛选掉非数字和字母的部分
while(!((s[i] >= 'a' && s[i] <= 'z') || (s[i] >= '0' && s[i] <= '9'))){
i++;
if(i >= j){
return true;
}
}
while(!((s[j] >= 'a' && s[j] <= 'z') || (s[j] >= '0' && s[j] <= '9'))){
j--;
if(i >= j){
return true;
}
}
if(s[i] != s[j]){
return false;
}
else{
i++;
j--;
}
}
return true;
}
};6.有效的字母异位词
class Solution {
public:
bool isAnagram(string s, string t) {
int flag[26];
memset(flag , 0 , 26*sizeof(int));
for(int i = 0; i < s.length() ; i++){
flag[s[i]-'a']++;
}
for(int i = 0; i < t.length(); i++){
flag[t[i]-'a']--;
}
for(int i = 0; i < 26 ;i++){
if(flag[i] != 0){
return false;
}
}
return true;
}
};class Solution {
public:
int firstUniqChar(string s) {
int flag[26];
memset(flag , 0 , 26*sizeof(int));
for(int i = 0; i < s.length() ; i++){
flag[s[i]-'a']++;
}
for(int i = 0; i < s.length() ; i++){
if(flag[s[i]-'a'] == 1){
return i;
}
}
return -1;
}
};8.反转字符串
class Solution {
public:
void swap(char &s1 , char &s2){
char tmp = s1;
s1 = s2;
s2 = tmp;
}
void reverseString(vector<char>& s) {
int i = 0;
int j = s.size() - 1;
while(i < j){
swap(s[i] , s[j]);
i++;
j--;
}
}
};