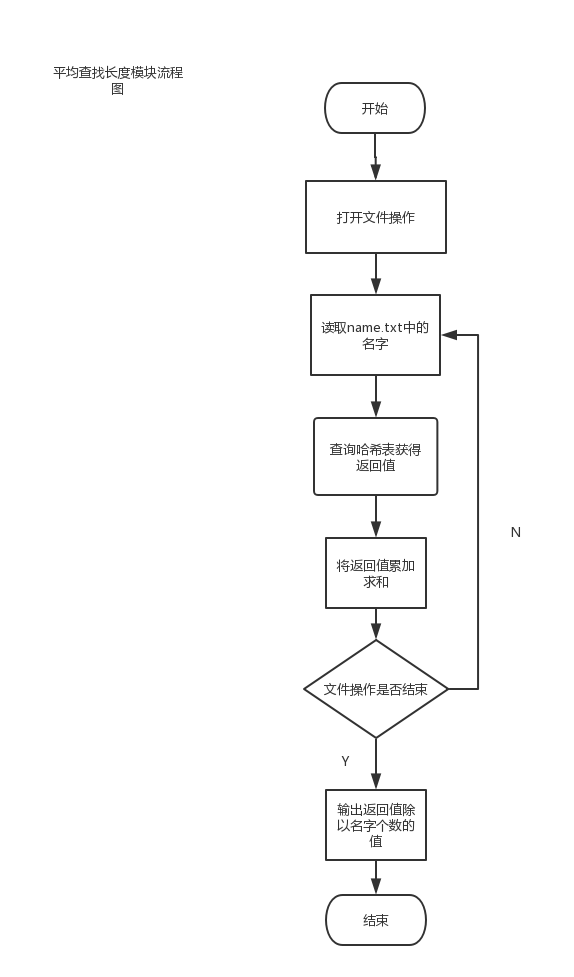
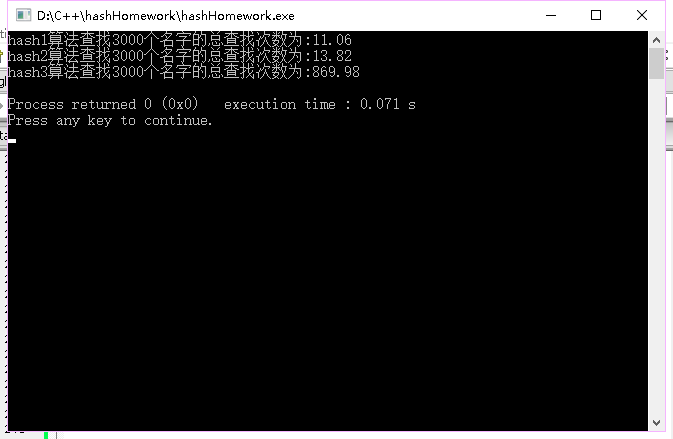
要求:
- 利用随机函数产生N个随机整数(20000个以上),对这些数进行多种方法排序;
- 采用插入排序、希尔排序、冒泡排序、快速排序、选择排序、堆排序、归并排序方法实现上述方法求解;
- 把排序后的结果保存在不同的文件中;
- 统计每一种排序方法的性能,以上机运行程序所花费的时间为准进行对比;
- 找出其中两种较快的方法。
排序算法可以说是一项基本功,解决实际问题中经常遇到,针对实际数据的特点选择合适的排序算法可以使程序获得更高的效率,有时候排序的稳定性还是实际问题中必须考虑的。
需求分析
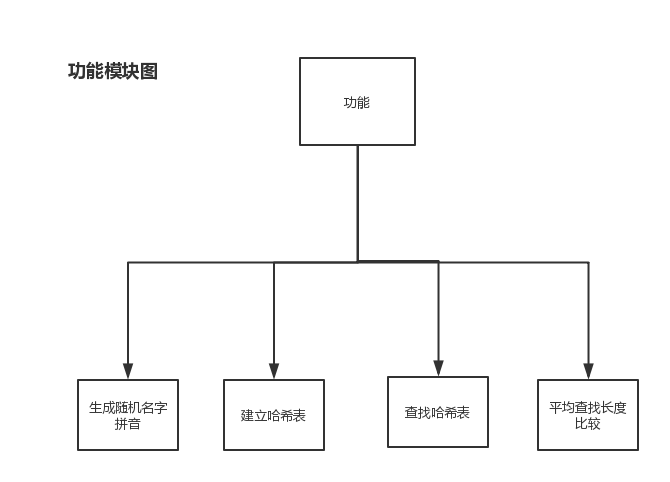
我们的程序需要实现几个模块,其中包括
- 产生随机数模块
- 多种方法排序模块
- 比较排序性能模块
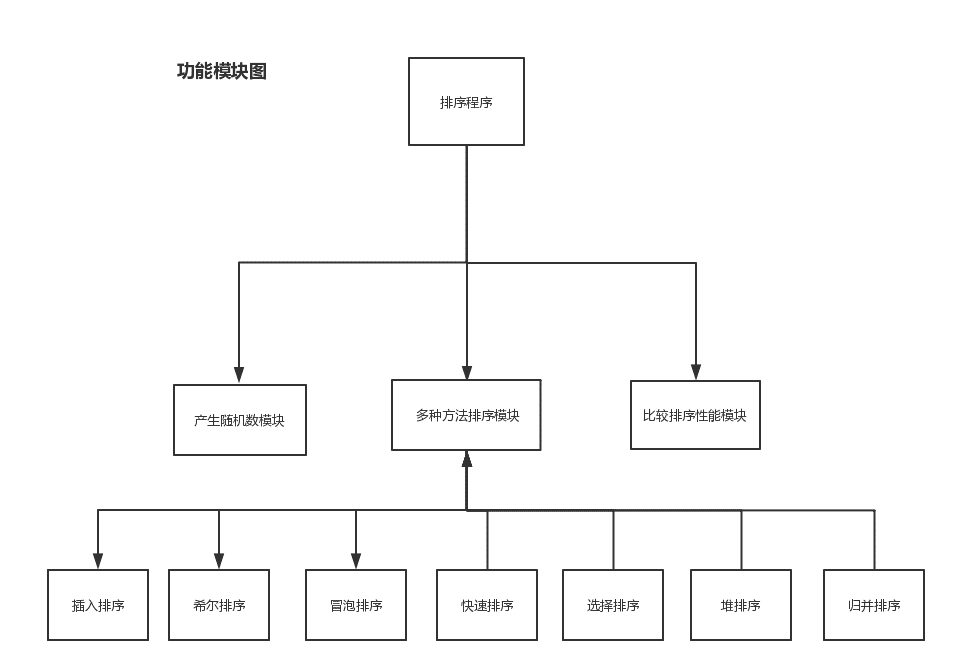
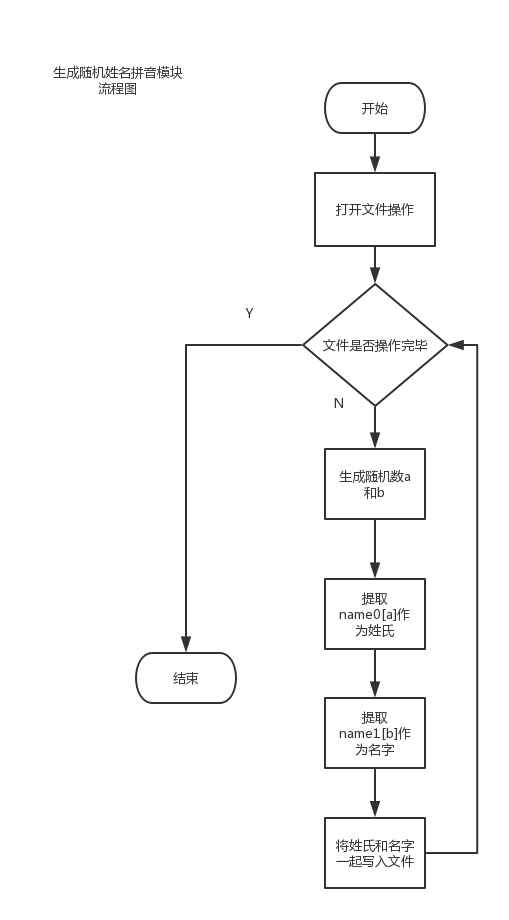
产生随机数模块可以通过C++的rand()函数随机生成伪随机数,并将这20000个随机数存在一个名为number.txt的文件中。
然后在程序中实现插入排序、希尔排序、冒泡排序、快速排序、选择排序、堆排序、归并排序等排序方法以完成多种方法排序模块。
然后通过执行不同的排序算法所花费的时间进行比较,得出最快的两种方法,并得出以上排序算法的性能排名。
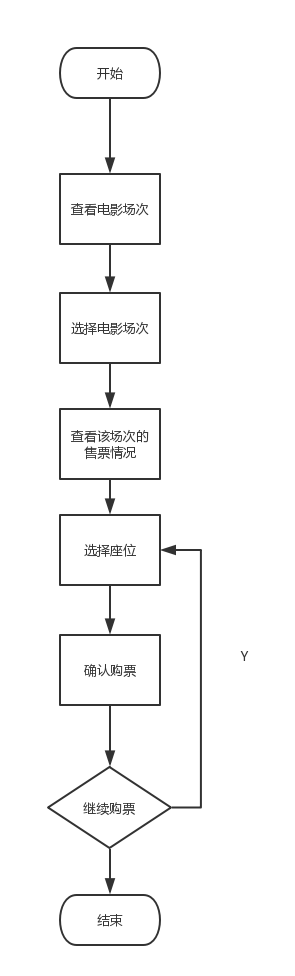
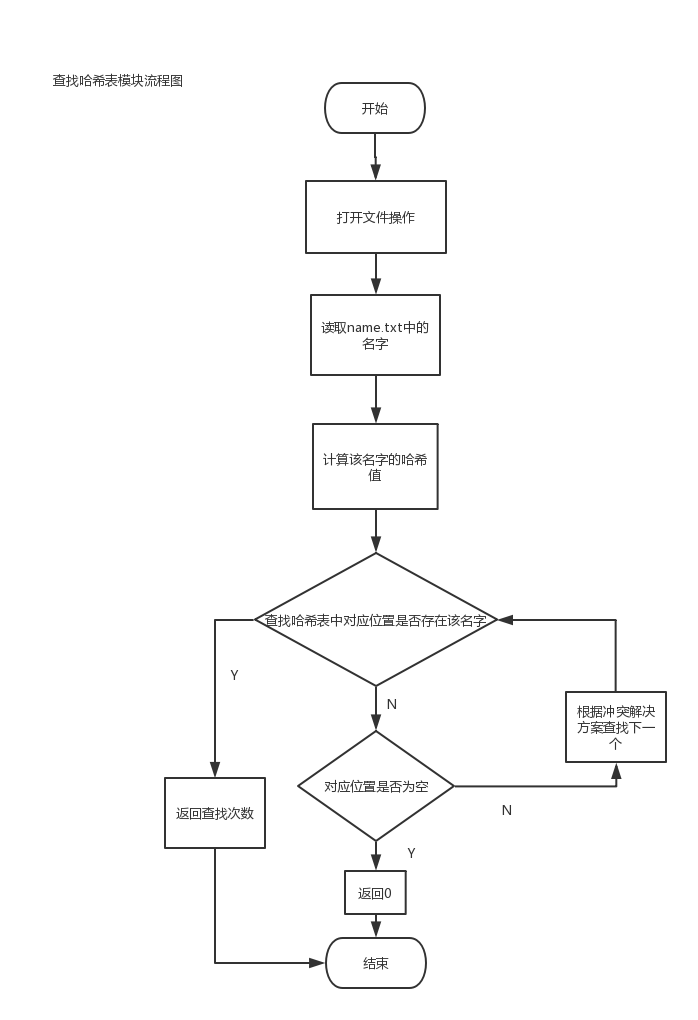
程序流程图:
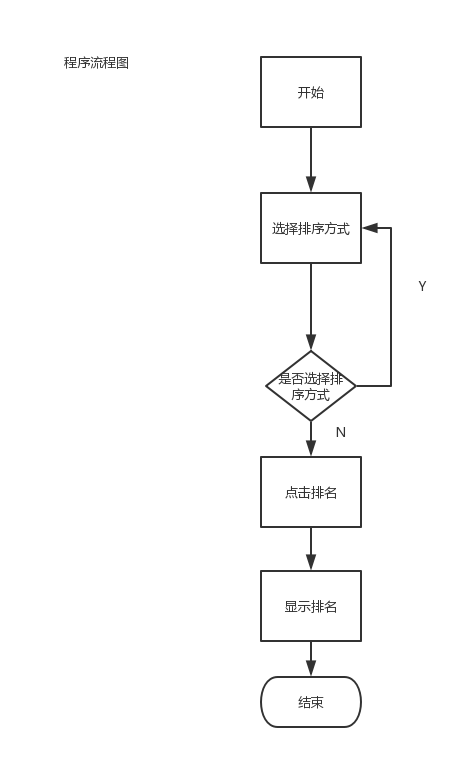
系统设计
开发环境:
操作系统:Microsoft Windows 10 64位
IDE:CodeBlocks 32位
编译器:GNU GCC Compiler
编程语言:C++
图形库:ACLLib
数据结构:
本程序使用了顺序表来存储所有的数据,并基于顺序表的结构进行排序。
同时,本程序使用了ACLLib图形库画出了简单的图形界面,使我们的性能对比更加直观。
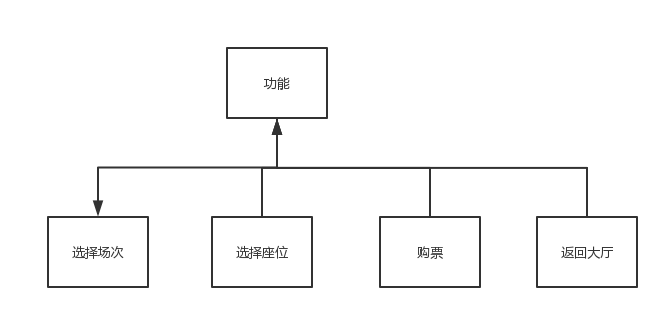
函数调用关系图:

排序算法伪代码:
插入排序:
for i←2 to n
x←A[i]
j←i-1
while(j>0) and (A[j]>x)
A[j+1]←A[j]
j←j-1
end while
A[j+1]←x
end for
希尔排序:
input: an array a of length n with array elements numbered 0 to n − 1
inc ← round(n/2)
while inc > 0 do:
for i = inc .. n − 1 do:
temp ← a[i]
j ← i
while j ≥ inc and a[j − inc] > temp do:
a[j] ← a[j − inc]
j ← j − inc
a[j] ← temp
inc ← round(inc / 2.2)
冒泡排序:
BubbleSort(input ele[],input length)
for i <- 1 to length step 1
for j <- i+1 to 0 step -1
if ele[j] < ele [j – 1]
swap (ele[j],ele[j – 1])
end if
end
end
快速排序:
if low<high then
SPLIT(A[low…high],w) //w为A[low]的新位置
quicksort(A,low,w-1)
quicksort(A,w+1,high)
end if
选择排序:
for i←1 to n-1
k←i //设立标志位
for j←i+1 to n //查找第i小的元素
if A[j]<A[k] then k←j
end for
if k≠i then 交换A[i]与A[k]
end for
堆排序:
1.下标计算[为与程序对应,下标从0开始]
Parent(i)://为了伪代码描述方便
returni/2
Left(i):
return2*i+1
Right(i):
return2*i+2
2.使下标i元素为根的的子树成为最大堆
MAX_HEAPIFY(A,i):
l<——Left(i)
r<——Right(i)
ifl<length(A)andA[l]>A[i]
thenlargest<——l
elselargest<——i
ifr<length(A)andA[r]>A[largest]
thenlargest<——r
iflargest!=i
thenexchangeA[i]<——>A[largest]//到这里完成了一层下降
MAX_HEAPIFY(A,largest)//这里是递归的让当前元素下降到最低位置
3.最大堆的建立,将数组A编译成一个最大堆
BUILD_MAX_HEAP(A):
heapsize[A]<——length[A]
fori<——length[A]/2+1 to0
MAX_HEAPIFY(A,i)//堆排序的开始首先要构造大顶堆,这里就是对内层节点进行逐级下沉(小元素)
4.堆排序
HEAP_SORT(A):
BUILD_MAX_HEAP(A)
fori<——length[A]-1to1//这里能够保证堆大小和数组大小的关系,堆在每一次置换后都减一
doexchangeA[1]<——> A[i]
length[A]<——length[A]-1
MAX_HEAPIFY(A,0)//对交换后的元素下沉
归并排序:
mergesort(A,1,n)
if low<high then
mid←⌊(low+high)/2⌋
mergesort(A,low,mid)
mergesort(A,mid+1,high)
MERGE(A,low,mid,high)
end if
MERGE()
//B[p…r]是个辅助数组
s←p;t←q+1;k←p
while s≤q and t≤r
if A[s]≤A[t] then
B[k]←A[s]
s←s+1
else
B[k]←A[t]
t←t+1
end if
k←k+1
end while
if s=q+1 then B[k…r]←A[t…r]
else B[k…r]←A[s…q]
end if
A[p…r]←B[p…r]
系统实现
函数功能:
(1)void adjust(int arr[], int len, int index) // 递归方式构建大根堆(len是arr的长度,index是第一个非叶子节点的下标)
(2)void bubbleSort(int nums[],int n) //冒泡排序算法
(3)bool comp(const mysort &a,const mysort &b)//结构体的排序函数
(4)string doubleToString(double num)//double类型转string类型函数
(5)void heapSort(int nums[],int n) //堆排序算法
(6)void insertSort(int nums[],int n) //插入排序算法
(7)void makeRandNumber()//生成20000个随机数放在项目目录的number.txt下
(8)void Merge(int A[], int start, int mid, int step, int n)//归并排序算法
(9)void mergeSort(int nums[],int n) //递归进行归并排序
(10)void mouseListener(int x , int y ,int button ,int event){//监听函数,用来判断鼠标点击
(11)void quickSort(int b, int e, int a[])//快速排序算法
(12)void readNums(int nums[]) //读取文件中的数字到数组中
(13)void selectionSort(int nums[],int n) //选择排序算法
(14)int Setup()//ACLLib图形库进入Win32程序的入口函数
(15)void shellSort(int nums[],int n) //希尔排序算法
(16)void showIndex()//画出界面的首页
算法:
- 插入排序
思想:
每次选择一个元素K插入到之前已排好序的部分A[1…i]中,插入过程中K依次由后向前与A[1…i]中的元素进行比较。若发现发现A[x]>=K,则将K插入到A[x]的后面,插入前需要移动元素。
时间复杂度:
最好的情况下:正序有序(从小到大),这样只需要比较n次,不需要移动。因此时间复杂度为O(n)
最坏的情况下:逆序有序,这样每一个元素就需要比较n次,共有n个元素,因此实际复杂度为O(n2)
平均情况下:O(n2)
稳定性:
理解性记忆比死记硬背要好。因此,我们来分析下。稳定性,就是有两个相同的元素,排序先后的相对位置是否变化,主要用在排序时有多个排序规则的情况下。在插入排序中,K1是已排序部分中的元素,当K2和K1比较时,直接插到K1的后面,没有必要插到K1的前面,因为这样做还需要移动。因此,插入排序是稳定的。
实现代码:
void insertSort(int nums[],int n) //插入排序
{
//从第二个元素开始,加入第一个元素是已排序数组
for (int i = 1; i < n; i++)
{
//待插入元素 nums[i]
if (nums[i] < nums[i – 1])
{
int wait = nums[i];
int j = i;
while (j > 0 && nums[j – 1] > wait)
{
//从后往前遍历已排序数组,若待插入元素小于遍历的元素,则遍历元素向后挪位置
nums[j] = nums[j – 1];
j–;
}
nums[j] = wait;
}
}
}
- 希尔排序
思想:
希尔排序也是一种插入排序方法,实际上是一种分组插入方法。先取定一个小于n的整数d1作为第一个增量,把表的全部记录分成d1个组,所有距离为d1的倍数的记录放在同一个组中,在各组内进行直接插入排序;然后,取第二个增量d2(<d1),重复上述的分组和排序,直至所取的增量dt=1(dt<dt-1<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
时间复杂度:
最好情况:由于希尔排序的好坏和步长d的选择有很多关系,因此,目前还没有得出最好的步长如何选择(现在有些比较好的选择了,但不确定是否是最好的)。所以,不知道最好的情况下的算法时间复杂度。
最坏情况下:O(n*logn),最坏的情况下和平均情况下差不多。
平均情况下:O(N*logn),实际约为O(n(1.3—2))。
稳定性:
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
实现代码:
void shellSort(int nums[],int n) //希尔排序
{
int i, j;
int increment = n;
do
{
increment = increment / 3 +1;
for (i = increment ; i <= n – 1; i++)
{
if (nums[i] < nums[i – increment])
{
int tmp;
tmp = nums[i];
for (j = i – increment; j >= 0 && tmp < nums[j]; j -= increment)
nums[j + increment] = nums[j];
nums[j + increment] = tmp;
}
}
}
while (increment > 1);
}
- 冒泡排序
思想:
通过无序区中相邻记录关键字间的比较和位置的交换,使关键字最小的记录如气泡一般逐渐往上“漂浮”直至“水面”。
时间复杂度:
最好情况下:正序有序,则只需要比较n次。故,为O(n)。
最坏情况下: 逆序有序,则需要比较(n-1)+(n-2)+……+1,故,为O(N*N)。
稳定性:
排序过程中只交换相邻两个元素的位置。因此,当两个数相等时,是没必要交换两个数的位置的。所以,它们的相对位置并没有改变,冒泡排序算法是稳定的。
实现代码:
void bubbleSort(int nums[],int n) //冒泡排序
{
for(int i = 0; i<n-1; i++)
{
for(int j = i+1; j<n; j++)
{
if(nums[i]>nums[j])
{
swap(nums[i],nums[j]);
}
}
}
}
- 快速排序
思想:
它是由冒泡排序改进而来的。在待排序的n个记录中任取一个记录(通常取第一个记录),把该记录放入适当位置后,数据序列被此记录划分成两部分。所有关键字比该记录关键字小的记录放置在前一部分,所有比它大的记录放置在后一部分,并把该记录排在这两部分的中间(称为该记录归位),这个过程称作一趟快速排序。
时间复杂度:
最好的情况下:因为每次都将序列分为两个部分(一般二分都复杂度都和logN相关),故为 O(N*logN)。
最坏的情况下:基本有序时,退化为冒泡排序,几乎要比较N*N次,故为O(N*N)。
稳定性:
由于每次都需要和中轴元素交换,因此原来的顺序就可能被打乱。如序列为 5 3 3 4 3 8 9 10 11会将3的顺序打乱。所以说,快速排序是不稳定的。
实现代码:
void quickSort(int b, int e, int a[])
{
int i = b, j = e; //i是数组的头,j是数组的尾
int x = a[(b + e) / 2]; //选取数组的中间元素作为划分的基准
while (i<j)
{
while (a[i]<x) i++;
while (a[j]>x) j–;
if (i <= j)
std::swap(a[i++], a[j–]);
}
if (i<e)
quickSort(i, e, a);
if (j>b)
quickSort(b, j, a);
}
- 选择排序
思想:
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。以此类推,直到所有元素均排序完毕。具体做法是:选择最小的元素与未排序部分的首部交换,使得序列的前面为有序。
时间复杂度:
最好情况下:交换0次,但是每次都要找到最小的元素,因此大约必须遍历N*N次,因此为O(N*N),减少了交换次数。
最坏情况下,平均情况下:O(N*N)。
稳定性:
由于每次都是选取未排序序列A中的最小元素x与A中的第一个元素交换,因此跨距离了,很可能破坏了元素间的相对位置,因此选择排序是不稳定的。
实现代码:
void selectionSort(int nums[],int n) //选择排序
{
int i, j, minn;
for (i = 0; i < n – 1; i++)
{
minn = i; //记录最小值的下标,初始化为i
for (j=i+1; j<=n-1; j++)
{
if (nums[j] < nums[minn])
minn = j; //通过不断地比较,得到最小值的下标
}
swap(nums[i], nums[minn]);
}
}
- 堆排序
思想:
利用完全二叉树中双亲节点和孩子节点之间的内在关系,在当前无序区中选择关键字最大(或者最小)的记录。也就是说,以最小堆为例,根节点为最小元素,较大的节点偏向于分布在堆底附近。
时间复杂度:
最坏情况下,接近于最差情况下:O(N*logN),因此它是一种效果不错的排序算法。
稳定性:
堆排序需要不断地调整堆,因此它是一种不稳定的排序。
实现代码:
// 递归方式构建大根堆(len是arr的长度,index是第一个非叶子节点的下标)
void adjust(int arr[], int len, int index)
{
int left = 2*index + 1; // index的左子节点
int right = 2*index + 2;// index的右子节点
int maxIdx = index;
if(left<len && arr[left] > arr[maxIdx]) maxIdx = left;
if(right<len && arr[right] > arr[maxIdx]) maxIdx = right;
if(maxIdx != index)
{
swap(arr[maxIdx], arr[index]);
adjust(arr, len, maxIdx);
}
}
void heapSort(int nums[],int n) //堆排序
{
// 构建大根堆(从最后一个非叶子节点向上)
for(int i=n/2 – 1; i >= 0; i–)
{
adjust(nums, n, i);
}
// 调整大根堆
for(int i = n – 1; i >= 1; i–)
{
swap(nums[0], nums[i]); // 将当前最大的放置到数组末尾
adjust(nums, i, 0); // 将未完成排序的部分继续进行堆排序
}
}
- 归并排序
思想:
多次将两个或两个以上的有序表合并成一个新的有序表。
时间复杂度:
最好的情况下:一趟归并需要n次,总共需要logN次,因此为O(N*logN) 。
最坏的情况下,接近于平均情况下,为O(N*logN) 。
说明:对长度为n的文件,需进行logN 趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。
稳定性:
归并排序最大的特色就是它是一种稳定的排序算法。归并过程中是不会改变元素的相对位置的。
实现代码:
void Merge(int A[], int start, int mid, int step, int n)
{
int rightLen = 0;
if (mid + step > n)
{
rightLen = n – mid;
}
else
{
rightLen = step;
}
//申请空间存放临时结果
int *tempArray = new int[step + rightLen]();
int i = 0, j = 0, k = 0;
while (i < step && j < rightLen)
{
if (A[start + i] < A[mid + j])
{
tempArray[k++] = A[start + i];
i++;
}
else
{
tempArray[k++] = A[mid + j];
j++;
}
}
//如果左边没有归并完,那么直接将剩余的元素复制到tempArray的后面
if (j == rightLen)
{
memcpy(tempArray + i + j, A + start + i, (step – i) * sizeof(int));
}
//如果右边没有归并完,那么直接将剩余的元素复制到tempArray的后面
else if (i == step)
{
memcpy(tempArray + i + j, A + mid + j, (rightLen – j) * sizeof(int));
}
//将临时数组中排好序的内容复制回原数组
memcpy(A + start, tempArray, (step + rightLen) * sizeof(int));
delete[] tempArray;
}
void mergeSort(int nums[],int n) //归并排序
{
for (int step = 1; step < n; step *= 2)
{
for (int i = 0; i < n – step; i += 2*step)
{
Merge(nums ,i, i+step, step, n);
}
}
}
最后,排序其实是有改进方法的,最近研究了一下。
快速排序主要有以下几种改进方法:
快速排序基本思路:找到一个标定点,左边的元素小于标定点,右边元素大于标定点,然后再对左右区间递归快速排序。
改进1:如果数组近乎有序,标定点的选择会影响快速排序的性能,如果每次都选择最小值作为标定点,快速排序时间复杂度会退化为O(N*N),因此需要随机化标定点元素。
改进2:如果数组有大量相同元素,上面的做法会将相同元素分到大于v的区间,会造成两个子区间元素不平衡,所以需要将相等元素平衡地分入两个区间。
改进3:可以改成三路快速排序算法。
当然,在我们程序中排名最慢的冒泡排序也是可以优化的,我们都知道,当一个序列已经有序的情况下,冒泡排序往往会做很多不必要的重复的比较,在此基础上我们能够优化一下。
优化:设置一个标志符flag,flag初始值是0,如果在一趟遍历中有出现元素交换的情况,那就把flag置为1。一趟冒泡结束后,检查flag的值。如果flag依旧是0,那这一趟就没有元素交换位置,说明数组已经有序,循环结束。
用户手册
首先运行我们的程序,界面如下:
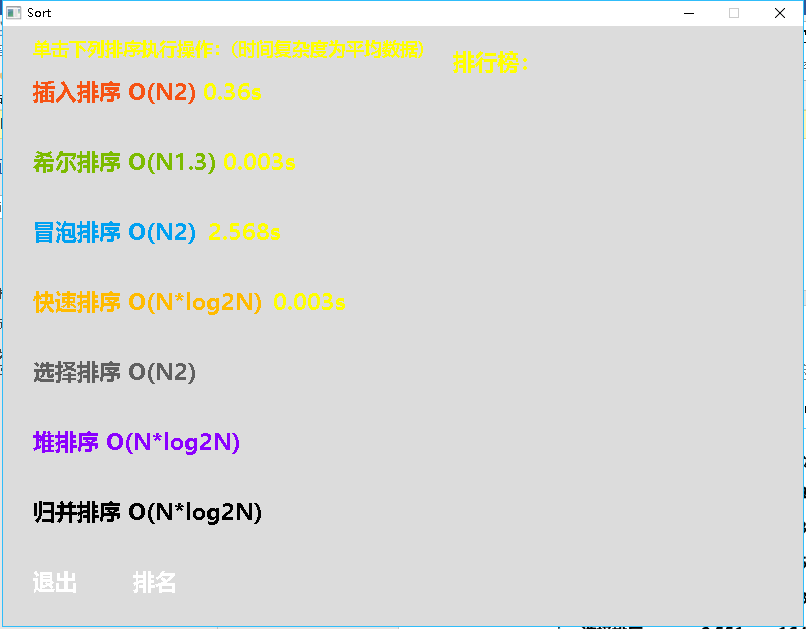
分别用鼠标左键单击插入排序、希尔排序、冒泡排序、快速排序、选择排序、堆排序、归并排序,界面会显示出我们执行相应的算法所花费的时间,如图所示:
与此同时,我们的项目目录下会多出一些文本文件,这些文本文件分别是各种排序算法的结果,我们用文本将结果保存下来,如图所示:
最后,我们点击排名,即可看到各种算法的性能比较排名,如图所示:

排序是软件设计中最常用的运算之一,有多种不同的算法,每种算法各有其特定性和最合适的适用范围。因此,了解这些特性对于实际应用时选择最恰当算法是软件设计中的重要技术。通过本次课程设计,我体会到了各种算法的性能特点,包括时间性能、空间性能以及排序的稳定性。同时,通过实验的方法来分析算法的各种性能是计算机科学与技术领域重要的手段,是研究各类问题求解的新算法所必需的技术,应引起足够的重视,可以看出在数据规模达到一定数目时,我们的冒泡排序算法相对于其他算法所花费的时间越来越多,由此可见算法的性能十分重要。经过测试我们发现在大部分情况下快速排序的效率都是极其高的,但当测试的数据为有序的时候,快排的效率便会降低,并且有可能造成栈溢出等问题。
当然,这里提一下我对排序算法的稳定性的理解,首先,排序算法的稳定性大家应该都知道,通俗地讲就是能保证排序前2个相等的数其在序列的前后位置顺序和排序后它们两个的前后位置顺序相同。在简单形式化一下,如果Ai = Aj, Ai原来在位置前,排序后Ai还是要在Aj位置前。其次,说一下稳定性的好处。排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。另外,如果排序算法稳定,对基于比较的排序算法而言,元素交换的次数可能会少一些。
最后,在这次课程设计中,我简单的学习了一下图形化编程,受益匪浅,程序不再由黑色的命令行框框组成,而是有趣的图形化界面,增加了我对于编程的兴趣,最后,我们的排序算法还有一些可以优化的地方,我会慢慢学习改进这些排序算法。
在这里我们研究学习的全部都是内部排序,那么外部排序是否也类似呢?在程序的世界里,我们往往在做一些分而治之的事情,通过对内部排序的初步学习和认识,我对外部排序也产生了浓烈的兴趣。
学习和生活中有好多地方都设计排序的问题,学好排序的相关知识很有用。